江苏省沭阳如东2024~2025学年第一学期九年级期末试卷
免费说明:开放式免费下载
分享下江苏省宿迁市沭阳如东2024~2025学年第一学期九年级期末试卷,需要的同学做一下吧。

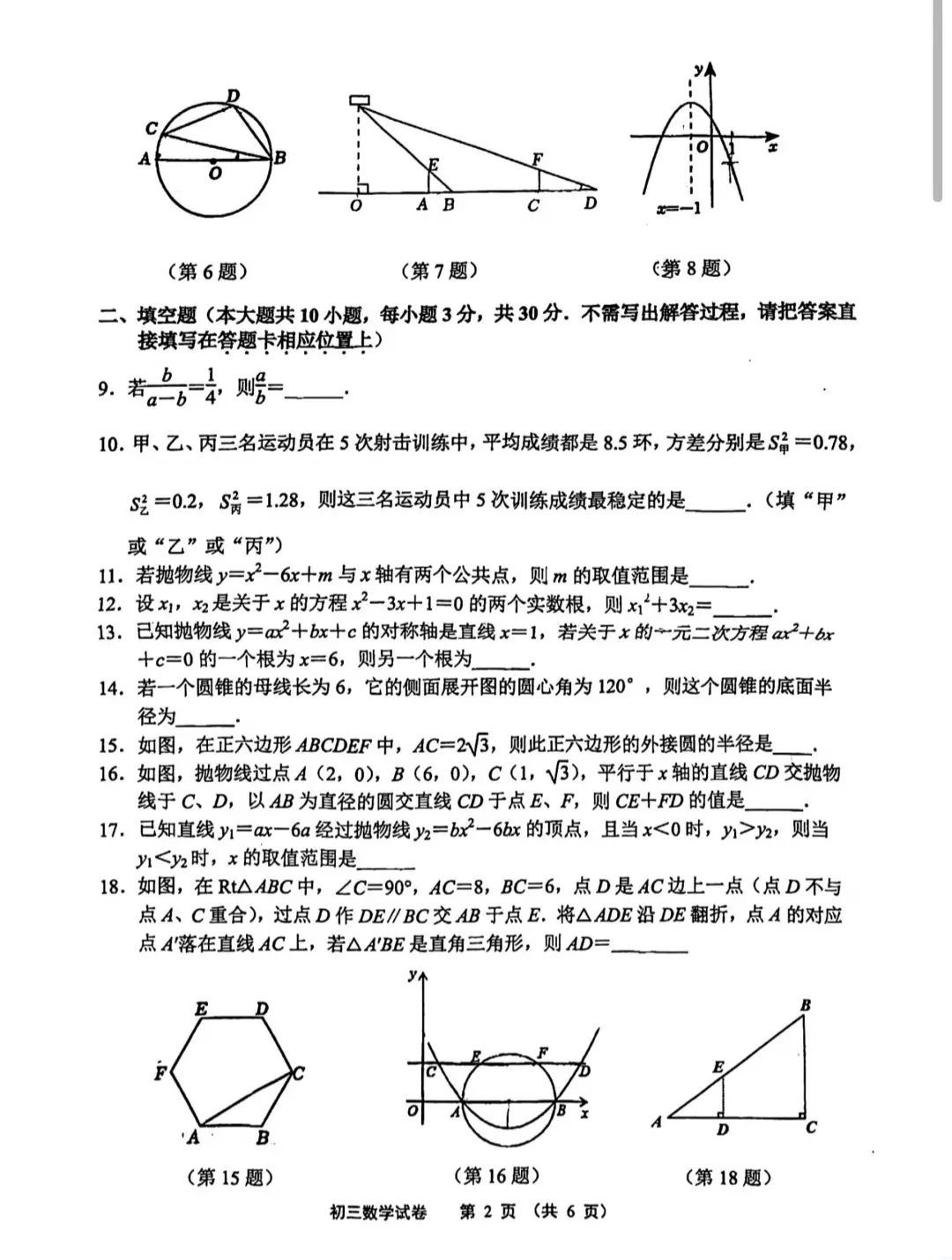
2024~2025学年度第一学期质量检测 初三数学试卷 本卷满分:150分 考试时间:120分钟 班级: 姓名: 一、选择题(本大题共8小题,每小题3分,共24分,在所给出的四个选项中,有且仅 有一项是符合题目要求的,请将正确选项的字母代号填写在答题卡相应位置上) 1.下列函数中,是二次函数的是() A.y=8x2+1 B.y=8x+1 C.y=8 D.y=+1 2.在一次演讲比赛中,某位选手的演讲内容、演讲表达的得分分别为90分,95分,将演 讲内容、演讲表达的成绩按4:6计算,则该选手的成绩是( ) A,94分 B.93分 C.92分 D.91分 3.用配方法解一元二次方程x2+6x+1=0,此方程可化为( A.Gc-32=8 B.x+3)}2=8 C.x+3}2=3 D.x-3)2=3 4.某种品牌的电动车经过四、五月份连续两次涨价,每辆售价由3000元涨到了3600元, 设平均每月涨价的百分率为x,根据题意可列出的方程是( A.3000(1+x)2=3600 B.30001-x}2=3600 C.3600(1+x2=3000 D.3600(1-x)}=3000 5.将抛物线y=22的图像先向下平移3个单位,再向右平移4个单位所得的解析式为 () A.y=2x-3)}+4 B.y=2+4)2+3 C.y=2x-4)2+3 D.y=20x-4)2-3 6.如图,AB为⊙O的直径,点C、D在⊙O上,若∠ABC=12°,则∠BDC的度数是() A.7 B.68° C.102 D.112 7.如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点0)5米的A处, 沿OA所在的直线行走到点C时,人影长度增长3米,小方行走的路程AC=() 米 A.7.5 B.7.2 C.6.6 D.5.7 8.二次函数y=aa2+bx+十c(a≠0)的图像如图,给出下列四个结论:①abc>0:②4a十c <2b:③3b+2c<0:④m(am+b)+b<a(m时-1);其中正确结论的个数是() A.1个 B.2个 C.3个 D.4个 初三数学试卷 第1页(共6页) (第6题) (第7题) (第8题) 二、填空题(本大题共10小题,每小题3分,共30分。不需写出解答过程,请把答案直 接填写在答题卡相应位置上) 9.若。6京 10.甲、乙、丙三名运动员在5次射击训练中,平均成绩都是8.5环,方差分别是S=0.78, S经=02,S%=128,则这三名运动员中5次训练成绩最稳定的是,(填“甲” 或“乙”或“丙”) 11,若抛物线y=x2-6x十m与x轴有两个公共点,则m的取值范围是 12.设,是关于x的方程x2-3x十1=0的两个实数根,则+3x2= 13.已知抛物线y=a2十bx十c的对称轴是直线x=1,若关于x的一元二次方程ax2+r 十+c=0的一个根为x=6,则另一个根为 14,若一个圆锥的母线长为6,它的侧面展开图的圆心角为120°,则这个圆锥的底面半 径为一 15.如图,在正六边形ABCDEF中,AC=2V,则此正六边形的外接圆的半径是 16.如图,抛物线过点A(2,0),B(6,0),C(1,V3),平行于x轴的直线CD交抛物 线于C、D,以AB为直径的圆交直线CD于点E、F,则CE十FD的值是 17.已知直线h=ar一6a经过抛物线2=bx2-6r的顶点,且当x<0时,>2,则当 h<2时,x的取值范围是 18.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D是AC边上一点(点D不与 点A、C重合),过点D作DE∥BC交AB于点E.将△ADE沿DE翻折,点A的对应 点A落在直线AC上,若△A'BE是直角三角形,则AD=一 22,(8分)在一只不透明的布袋中,装有质地、大小均相同的四个小球,小球上分别标有 数字1,2,3,4.甲乙两人玩摸球游戏,规则为:两人同时从袋中随机各摸出1个小 球,若两球上的数字之和为奇数,则甲胜:若两球上的数字之和为偶数,则乙胜. (1)请用画树状图或列表的方法,求甲获胜的概率 (2)这个游戏规则对甲乙双方公平吗?请说明理由, 23.(10分)如图,在△ABC中,∠ACB=90°,D为边AB上一点,且CD=CA,过点D 作DE⊥AB,交BC于点E. (1)求证:△CDE∽△CBD: (2)若AC=3,AB=5,求CE的长. 24.(10分)如图,在△ABC中,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图 中标明相应的字母,(保留作图痕迹,不写作法) (1)①作∠BAC的平分线,交BC于点O:②以O为圆心,OB为半径作圆: (2)在(1)中所作的图中,判断AC与⊙0的位置关系并说明理由: (3)若AB=3,BC=4,求⊙0的半径. 27.(12分)在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠, 顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F, (1)如图1,若点E是AD的中点,求证:△AEB≌△DEC: (2)如图2,当AD=25,且B<DE时,求是的值: (3)如图3,当BEEF=84时,求BP的值 G G D 图1 图2 图3 28.(12分)在平面直角坐标系中,抛物线y=a(x一1)2一2(a>0)如图所示,该抛物 线与x轴交于点A、B(点A在点B的左侧),OA=1,经过点A的直线y=a十b(0) 与y轴正半轴交于点C,且与抛物线的另一个交点为D,△ABD的面积为5. (1)求抛物线和直线的解析式: (2)抛物线上的动点E在直线的下方,求△ACE面积的最大值,并求出此时点E的 坐标: (3)若点P为x轴上任意一点,在(2)的结论下,求PE+PA的最小值,
样本阅读结束,请到下载地址中:阅读全文及下载