江苏省沭阳县老怀文2024~2025学年初二12.14月考数学真题卷

江苏省宿迁市沭阳县老怀文2024~2025学年初二12.14月考数学真题卷，三零论坛（30论坛）用百度云盘、腾讯云盘分享的八年级\江苏省\2024-2025学年上\宿迁市\数学月考原卷版、解析版及答案，在云盘中的课件资料可在线阅读及保存到自己的云盘，此电子版课件永久免费阅读及下载。

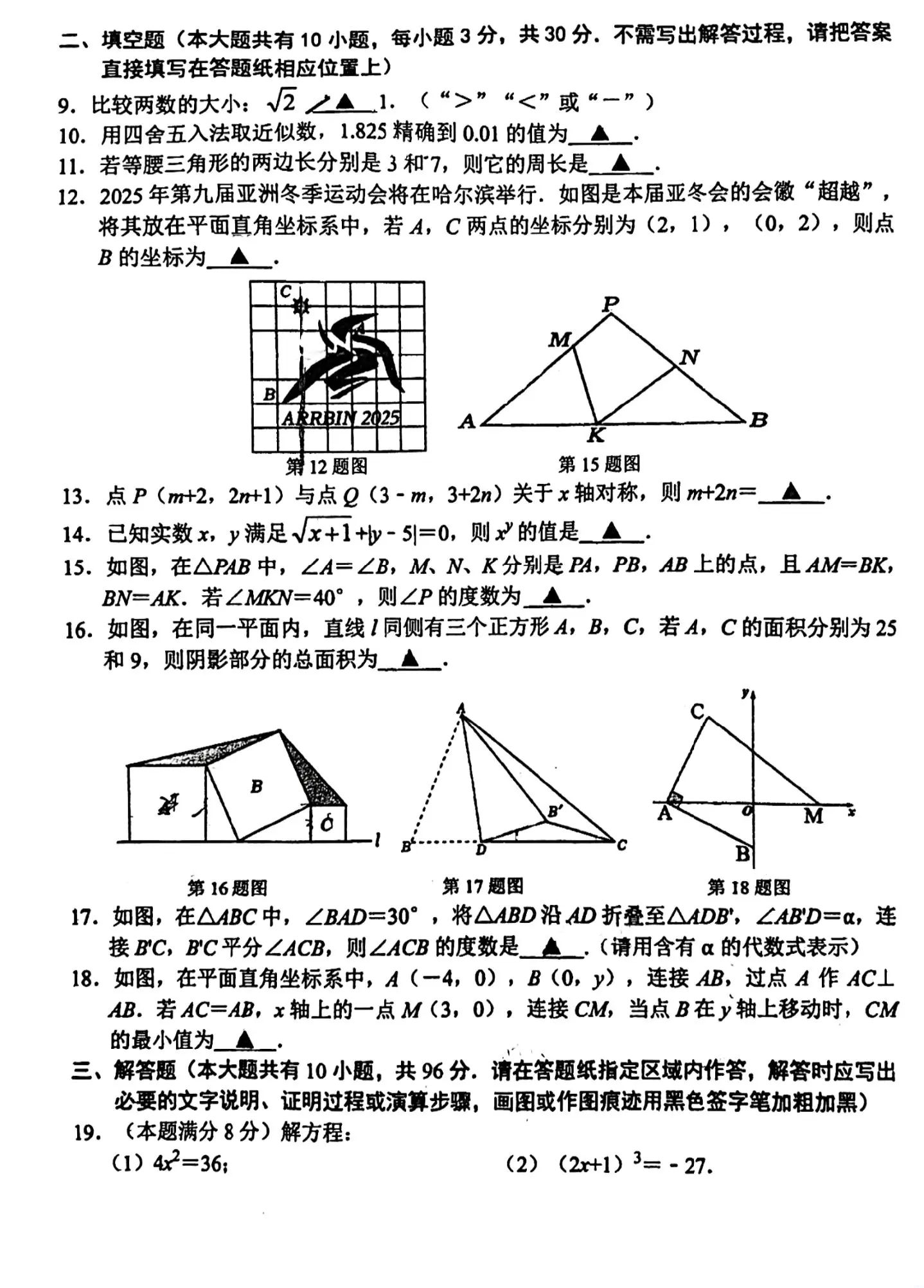
2024一2025学年度第一学期八年级
数学试卷
(总分：150分，时长：120分钟，日期：2024.12.13)
一、选择题（本大题共有8小题，每小题3分，共24分。在每小题所给出的四个选项中，
恰有一项是符合题目要求的，请将正确选项前的字母代号填写在答题纸相应位置上
1.在平面直角坐标系中，点(1，~2)所在的象限是（▲）
A.第一象限
B.'第二象限
C.第三象限
D.第四象限
2.我国是最早了解勾股定理的国家之一，它被记载于我国古代著名的数学著作《周碑算
经》中.下列各组数中，是“勾股数”的是（▲）
A.6,8,10
B.2,3,.5
C.4,5,6
D.1,2,5
3.在实数0.3,0，√万，，0.123456…
334
0.05.中，无理数的个数是（▲)
113
A.2
B.3
C.4
D.5
4.如图所示的图象分别给出了x与y的对应关系，其中能表示y是x的函数的是（▲）
A
5.如图，点E、点F在BC上，BE=CF,∠AFB=∠DEC,添加一个条件，不能说明
△ABF≌△DCE的是（▲）
A.AF=DE
B.AB=DC
C.∠B=∠C
D.∠A=∠D
第5题图
第6题图
6.如图，在△ABC中，ED∥BC,∠ABC和∠ACB的平分线分别交ED于点F、G,
若FG=2,ED=6,则DB+EC的值为（▲)
A.3
B.4
C.5
D.9
7.现定义运算“※”：对于任意实数a、b,都有a※b=2-b2,如3※4=32-42=-7.
若x※3=16，则实数x的值为（▲）
A,4或-4
B.7或·1
C.19或-13
D.±5
·在平面直角坐标系中，孔明做走棋的游戏，其走法是：棋子从原点出发，第1步向右
走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位
依此类推，第n步的走法是：当n能被3整除时，则向上走1个单位：当n被3除，余
数为1时，则向右走1个单位：当n被3除，余数为2时，则向右走2个单位，当走完
第2024步时，棋子所处位置的坐标是（▲）
A.(2023,674)
B.(2024,675)
C.(2025,674)
D.(2026.675)
二、填空题（本大题共有10小题，每小题3分，共30分，不需写出解答过程，请把答案
直接填写在答题纸相应位置上)
9.比较两数的大小：√5∠▲1.（“>”“<”或“一”)
10.用四舍五入法取近似数，1.825精确到0.01的值为▲一
11,若等腰三角形的两边长分别是3和7，则它的周长是▲
12.2025年第九届亚洲冬季运动会将在哈尔滨举行.如图是本届亚冬会的会徽“超越”，
将其放在平面直角坐标系中，若A,C两点的坐标分别为(2,1)，(0,2)，则点
B的坐标为▲
ARRBIN 2025
B
第12题图
第15题图
13.点P(m+2,2+1)与点2(3-m,3+2n)关于x轴对称，则m+2n=▲
14.已知实数x,y满足√x+1+地-5引=0，则的值是▲
15.如图，在△PAB中，∠A=∠B,M、N、K分别是PA,PB,AB上的点，且AM=BK,
BN=AK.若∠MON=40°，则∠P的度数为▲
16.如图，在同一平面内，直线1同侧有三个正方形A,B,C,若A,C的面积分别为25
和9，则阴影部分的总面积为▲一·
B
第16题图
第17题图
第18题图
17.如图，在△ABC中，∠BAD=30°，将△ABD沿AD折叠至△DB,∠BD=a,连
接BC,BC平分∠ACB,则∠ACB的度数是▲，（请用含有&的代数式表示）
18.如图，在平面直角坐标系中，A(（一4,0)，B(0,y),连接AB,过点A作AC⊥
AB.若AC=AB,x轴上的一点M(3,O),连接CM,当点B在y轴上移动时，CM
的最小值为▲
三、解答题（本大题共有10小题，共96分，请在答题纸指定区域内作答，解答时应写出
必要的文字说明、证明过程或演算步骤，画图或作图痕迹用黑色签字笔加粗加黑)
19.(本题满分8分)解方程：
(1)4x2=36:
(2)(2+1)3=-27.
24.(本题满分10分)
如图，在平面直角坐标系xOy中，A、B、C三点的坐标分别为(~5,4)、（-3，
0)、(0,2).
(1)画出△ABC:
(2)△MBC面积为▲i
(3)如图，△A'B'C'是由△4BC经过平移得到的.已知点P(a,b)为△ABC
内的一点，则点P在△4'BC内的对应点P'的坐标是一
(4)若有一个动点2在y轴上，则2B'+2C'的最小值是▲一·
25.(本题满分10分)
在学习《实数》内容时，我们估算带有根号的无理数的近似值时，经常使用“逐步
逼近”的方法来实现。“逐步通近”是数学思维方法的一种重要形式，主要通过构
造“拟对象”、逐步扩充元素、逐步扩充范围、放缩逼近：合力逼近等方式解决问
题.例如：估算√互的近似值时，利用“逐步通近”的方法可以得出1.4<√2.5.请
你根据阅读内容回答下列问题：
(1)N5介于连续的两个整数a和b之间，且a<b,那么a=▲，b=▲
(2)√万的整数部分是▲，小数部分是一
(3)己知2+√们的小数部分为，5-1的小数部分为少，求xy的值.

样本阅读结束,请到下载地址中：阅读全文及下载

本站内容来自用户云盘共享，不承担任何版权及质量等问题，如有侵犯到你的权利，请来信证明你的权利，本站将来24小时内断开链接。