【浙江卷】浙江省浙江强基联盟2024年8月高三返校联考(金太阳25-06C)(8.28-8.30),高中\高三\浙江省\2024-2025学年上\数学三零论坛(30论坛)用百度云盘、腾讯云盘分享的原卷版、解析版及答案,在云盘中的课件资料可在线阅读及保存到自己的云盘,此电子版课件永久免费阅读及下载。

1.解:B={0,1,2,3},.A∩B={0,1,2},答案为C
2.解:=1+31-1+30二=4+21=2+i,答案为A
1+i(1+i)(1-i)2
3.解:(=(罗-3,k=2k一3或k十2k一3=9,得k=3或k=4,“k-3”是“(特=(-”的充
分不必要条件,答案为A
4.解:y=2x为奇函数,.g(x)=c十acr也为奇函数,得g(.r)Tg(一x)=c心十ae十cr十
ae=(a十1)(e十er)=0,.a=一l,答案为B.
5.解:”等差数列a)的前n项和为S,公差为d(丹}是公差为号的等若数列.又子-受-
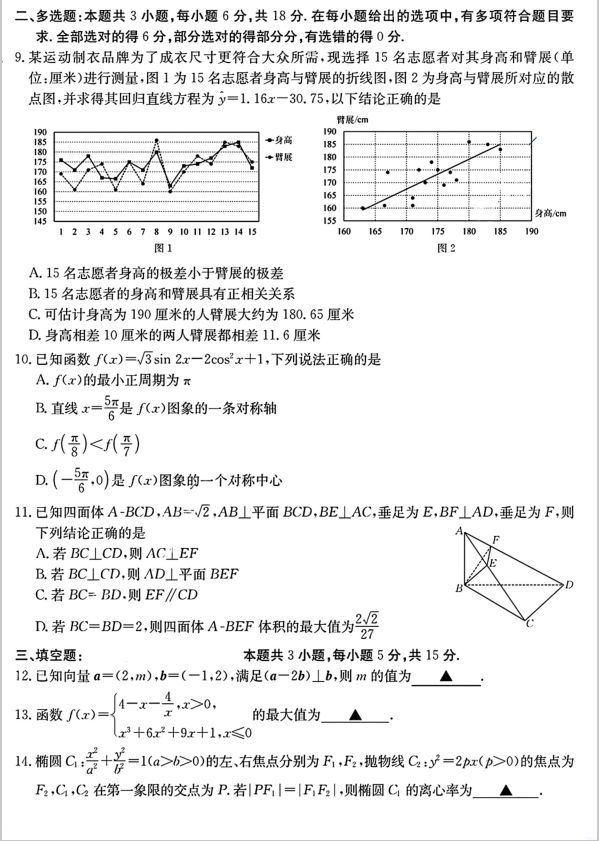
d=2,a1=1,∴.an=2n-1,a,=7,答案为D.
6.解:,acos B十bcos A=2 ccos C,由正弦定理可知sin Acos B+sin Bcos A=sin(A+B)=
sinC=2 2sin CosC,∴cosC=号∴C-602.义+e2-a2=2c,由余弦定理可知cosA=
士振4-要A=5B=5,
2bc
答案为C.
7.解:a=-e-号b=loe是>日<E-1<ia<<b,答案为B
8.解:设BP=t,DQ=t,则tan∠BAP=t,tan∠DAQ=t2,又∠BAP十
∠DAQ-登-子--1PQ=0-+a--
Q
√(t+t)=t十t2,又PC=1一t1,QC=1一t,∴三角形CPQ的周长为
定值2,答案为B.
B
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9
10
11
AB
ABC
BCD
9.解:对于A,身高的极差大约为21厘米,臂展的极差大约为26厘米,故A正确:对于B,山散
点图以及回归直线知,身高矮一些,臂展就会短一些,身高高一些,臂展就会长一些,故B正
确:对于C,身高为190厘米,从图象上明显得到臂展大于180.65厘米,故C错误:对于D,身
高相差10厘米的两人臂展的估计值相差11.6厘米,但并不是准确值,问归直线上的点并不
都是准确的样本点
,故D错误.答案为AB.
10.解:fx)=3sim2x-2osx+1=5in2x-c0s2x=2sin(2x-晋).对于A,T=2经=x,
故A正确:对于B,当x爱时,2x一吾=警-吾=受,故B正确:对于Cfx)在(-吾,5)
上单调递增,-晋<受<号<受(爱)<(),故C正确:对于D,当x=-爱时,2x一音
=-受-晋=-1,枚D不正确答案为ABC
11.解:对于A与B,BC⊥CD,CD⊥AB,CD⊥平面ABC,即CD⊥BE,即BE⊥平面ACD,BE
⊥AD,山题意得BF⊥AD,ADL平面BEF,AD LEF,即AC与EF不垂直,故A不正
确,B正确:对于CC=BD,△ABC2△ABD是-铝EF/CD,放C正确:对于D,
在△ABC中,可求得能-品-片Vg=y,又当且仅当∠DBC=90时,Vwm
有最大值号×号×2X2X厄-2.四面休4BEF休积的最大值为号,故D正确,答索
为BCD.
三、填空题:本题共3小题,每小题5分,共15分
02.613.114.3
12.解:a-2b=(4,m-4),(a-2b)·b=-4+2m-8=0,∴.m=6.
13.解:当x>0时,f(x)=4-(x1)≤4-1=0:当x≤0时,了(x)=32+12x+9=3(x+
1)·(x+3),f(x)在(一,一3),(一1,0)上单调递增,在(一3,一1)上单调递减,f(x)=
max{f(-3)./(0)}=1.综上所述,f(x)的最大值为1.
14.解:如图,由题意得F,F2=2c,PF2=2a-2c=PQ,FM=PQ=
2a-2c.F:M=4c-2a,PF-MF=PF-MF,(2c)2-(2a
-2c)2=(2a-2c)2-(4c-2a)2,化简得a2=3c2,即e=S
3
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过
程或演算步骤。
BX0=3X号=2
13分
16.(1)证明:连接BD,交EF于点G,交AC于点O,
E,F分别为AB,BC的巾点∴BG=BD,
又P-Pi,PB∥GQ
4分
又,'PB¢平面EFQ,GQC平面EFQ.
∴.PB∥平面EFQ
6分
(2)解:,四棱锥P-ACD为正四棱锥,(O为底而中心,以()为原点,建立如图所示的空间
直角
坐标系,
A(0,-√2,0),B(√2,0,0),C(0,√2,0),D(-√2,0,0),P(0,0w2),…9分
则BP=(-√2,0√2),AC=(0,2√2,0).
设平而EFQ的法向量为n=(x,y,),
B2,n=0,-√2x十√2z=0,
。得
AC.n=0,2W2y=0,
得n=(1,0,1).…
12分
平面ABCD的一个法向量为m一(0,0,1).
义.MN⊥平而EFQ,n∥MN,设MN与Ψ面ABD所成的角为0,
则sin0=cos(n,m》
n·m
1
②
nm
1X√2
14分
∴.MN与平面ACD所成的角为45°.
15分
9
8
1.解:1设C-芳-1,由题意可得2
=1,
a=1,
解得
1a2+b=2,
b=1,
.双曲线C的方程为x2一y2=1.
5分
(2)当过点A所作圆E:(x一2)2+y=1的切线斜率不存在时,
不妨设切线AN的斜率不存在,则直线AN的方程为x=3,
∴.xw=3,yw=-2√2,枚|AN|=1V2.
8分
当过点A所作圆E:(x一2)2十y2=1的切线斜率存在时,
设切线AM的方程为y一2√2=k(x一3),
则圆心E到直线AM的距离d=一十2②=1,解得k=72
样本阅读结束,请到下载地址中:阅读全文及下载